Riassunto

Parte 1

Logica

Operatori logici:

• ¬ = NOT
• ∨ = OR disgiunzione
• ∧ = AND congiunzione
• $\Rightarrow$ = implica
• ⇔ = doppia implicazione

---

Dati $P_1$ e $P_2$ proposizioni logiche:

• $P_2$ ∨ ¬$P_2$ è una tautologia
• $P_2$ ∧ ¬$P_2$ è insoddisfacibile
• $\neg (\neg P_1)\equiv P_1$
• $P_1\iff P_2\equiv (P_1\Rightarrow P_2)\wedge (P_2\Rightarrow P_1)$
• $P_1\Rightarrow P_2\equiv \neg P_1\vee P_2$
• $\neg (P_1\vee P_2)\equiv \neg P_1\wedge \neg P_2$
• $\neg (P_1\wedge P_2)\equiv \neg P_1\vee \neg P_1$

---

• CNF (Forma normale congiuntiva) = AND di vari OR
• DNF (Forma normale disgiuntiva) = OR di vari AND
• ✨metodo Di Bella ✨

---

Insiemi

Un insieme è una collezione ben definita di oggetti

• $x\in T$ = x appartiene all’insieme $T$
• $x\notin T$ = x non appartiene all’insieme $T$

---

• Insiemi uguali: $A=B\iff (\forall x)(x\in A\iff x\in B)$ A è uguale a B se e solo se qualsiasi x che appartiene ad A appartiene anche a B

---

• Possiamo definire un’insieme specificando le proprietà dei suoi elementi. Supponiamo che $P$ sia la proprietà di essere un numero pari minore di 10 allora $A=\{x\in N\mid x$ eˋ pari e $x<10\}$ ovvero $A=\{0,2,4,6,8\}$

---

• Cardinalità: definiamo cardinalità il numero di elementi che costituisce un insieme e si dento con: $|A|$

---

• Sottoinsieme: A ⊆ B ⇔ (∀x)(x ∈ A ⇒ x ∈ B) A è un sottoinsieme di B se e solo se qualunque x che appartiene ad A, appartiene anche a B

• Sovrainsieme: B ⊇ A ⇔ (∀x)(x ∈ A ⇒ x ∈ B) A è un sovrainsieme di B se e solo se qualunque x che appartiene ad A, appartiene anche a B

---

1. Unione: $A$ ∪ $B$ = {$x$ : $x\in A$ oppure $x\in B$.} $A$ unito $B$ è formato da qualsiasi $x$ che appartiene ad $A$ oppure a $B$
2. Intersezione: $A\cap B$ = {$x$ : $x\in A$ e $x\in B$.} $A$ intersezione $B$ è formata dalle x che appartengono sia ad $A$ che a $B$
3. Differenza: $A\backslash B$ = {x : x ∈ A e $x\notin B$.} $A$ differenza $B$ è formato dalle $x$ che appartengono ad $A$ ma non appartengono a B
4. Complemento: $U\backslash A$ dove $U$ è l’insieme universo
5. Differenza simmetrica: $A∆B=(A\backslash B)\cup (B\backslash A)$ è l’unione tra la differenza fra gli insiemi

Scritta matematicamente	Scritta logicamente
$A^C$	$\neg A$
$A\cup B$	$A\vee B$
$A\cap B$	$A\wedge B$
$(A\setminus B)$	$(A\wedge \neg B)$
$A△B=(A\setminus B)\cup (B\setminus A)$	$(A△B)\equiv (A\wedge \neg B)\vee (B\wedge \neg A)$

---

• $A\subseteq B$ o $B\subseteq A$: Per dimostrarlo si considera un elemento generico x ∈ A e si dimostra che x ∈ B
• $A=B$: Per dimostrarlo dobbiamo dimostrare che hanno gli stessi elementi. Quindi si dimostra che A ⊆ B e B ⊆ A.
• $A=\varnothing$: Per dimostrarlo si fa vedere che la definizione di appartenenza ad A porta ad una contraddizione.

---

Insieme delle parti: Dato un’insieme $T$ consideriamo insieme delle parti di $T$ un’insieme che contiene tutti i sottoinsiemi di $T$ e lo denotiamo così: $pow(T)$, $|pow(T)|=2^n$ è il numero di elementi di $T$, l’insieme delle parti ha le seguenti proprietà:

• $P(A\cap B)=P(A)\cap P(B)$

Dimostrazione

Per dimostrare che è vera l’equivalenza dobbiamo dimostrare 2 casi:

1. Caso ⊂: supponendo che $X\in P(A\cap B)$ e quindi che $X\subset A$ e $X\subset B$ da questo capiamo facilmente che $X\in P(A)$ e $X\in P(B)$ e quindi che $X\in P(A)\cap P(B)$

2. Caso ⊃: supponiamo che $X\in P(A)\cap P(B)$ e quindi che $X\subseteq A$ e $X\subseteq B$ quindi $X\subseteq A\cap B$ ciò implica che $X\in P(A\cap B)$

• $P(A\cup B)\supset P(A)\cup P(B)$

Dimostrazione

Per dimostrare questa formula dobbiamo dimostrare che $P(A\cup B)\supset P(A)\cup P(B)$ ma anche che un generico elemento di $P(A\cup B)$ non appartenga a $P(A)\cup P(B)$

1. Caso ⊃: Supponiamo che $X\in P(A)\cup P(B)$, allora $X\in P(A)$ oppure $X\in P(B)$.Nel primo caso $X\subseteq A$ mentre nel secondo caso $X\subseteq B$. In entrambi i casi, quindi, $X\subseteq A\cup B$ da cui $X\in P(A\cup B)$.

2. Caso $\ne$ : Sia A = {1, 2} e B = {1, 3}. L’insieme $A\cup B$ = {1, 2, 3} appartiene a $P(A\cup B)$ ma non appartiene a $P(A)$ ∪ $P(B)$ ( ricordiamo che P(A) = { ∅, {1}, {2}, {1,2} } invece P(B) = { ∅, {1}, {3}, {1,3} } )

---

• Famiglia di insiemi: sarebbe un insieme di insiemi (ES: l’insieme delle parti)

---

• Insiemi chiusi: Sia dato un insieme $U$ ed un operazione, se quest’ultima può essere definita o completata in $U$ allora possiamo dire che $U$ e chiuso rispetto a quell’operazione

---

Sia $F$ una famiglia di insiemi (Tipica forma di $F$ = $\{\{1\},\{2,3\},\{1,2\}\}$):

• Chiusura rispetto all’unione: diciamo che $F$ è chiusa rispetto all’unione se per ogni coppia di insiemi $X$ e $Y$ appartenenti a $F$ anche $X\cup Y$ appartiene a $F$.
• Chiusura rispetto all’intersezione: diciamo che $F$ è chiusa rispetto all’intersezione se per ogni coppia di insiemi $X$ e $Y$ appartenenti a $F$ anche $X\cap Y$ appartiene a $F$.
• $F^C$ = {$X^C$ : $X$ ∈ $F$ } ovvero come l’insieme di tutte le $X$ ∈ $F$ però complementate ($X$).
• La famiglia $F$ è chiusa rispetto all’unione se e solo se la famiglia $F^C$ è chiusa rispetto all’intersezione.
• La famiglia $F$ è chiusa rispetto all’intersezione se e solo se la famiglia $F^C$ è chiusa rispetto all’unione.

Dimostrazione

---

• Partizioni: Una famiglia di insiemi $F$ formata da sottoinsiemi dell’insieme universo $U$ può essere chiamata anche partizione di $U$

---

• Insieme prodotto: $A\times B$ = $\{(x,y):x\in A$ e $y\in B\}$ $A\times B$ è l’insieme di tutte le coppie $(x,y)$ con $x$ che appartiene ad $A$ e $y$ che appartiene a $B$

---

Diagramma di Venn: le regioni del diagramma di Venn sono $2^n$ qui

---

Paradosso di Russell: Partendo dal concetto di insieme, possiamo benissimo costruire un insieme formato da tutti quegli elementi che non appartengono a se stessi e lo definiamo in questo modo:

• $S=\{A:A\text{ eˋ un insieme, e }A\notin A\}$ $S$ è l’insieme di tutti gli insiemi che non appartengono a se stessi. Usando questa definizione $S\in S$?
• Se diciamo SI: Se $S$ appartiene a se stesso, allora per definizione di S, S non dovrebbe appartenere a se stesso (perché S contiene solo insiemi che non appartengono a se stessi). Questo è una contraddizione.
• Se diciamo NO: Se $S$ non appartiene a se stesso, allora per definizione di $S$, $S$ dovrebbe appartenere a se stesso (perché $S$ contiene tutti gli insiemi che non appartengono a se stessi). Anche in questo caso abbiamo una contraddizione.

---

Relazioni e funzioni

Relazione: $R\subseteq U\times U$ ovvero un sottoinsieme dell’insieme prodotto $U\times U$ ovvero: $\{(x,y)\in U\times U:R(x,y)$ è vera$\}$ in altre parole un insieme formato da tutte le coppie ordinate che rendono vera la relazione. Proprietà qui

---

Funzione: Una relazione $f$ definita su $A\times B$ si dice funzione da $A$ (dominio) in $B$ (codominio) se per ogni $x\in A$ esiste uno ed uno solo $y\in B$ tale che $(x,y)\in f$ e quindi che $f(x)=y$.

---

Definizioni:

• $f:A\to B$ per ogni $x$, $f(x)=x$ si dice applicazione identica di $A$
• $f:A\times B\to A$ tale che per ogni $(x,y)$ $f(x,y)$ = $x$ si dice proiezione canonica su $A$.
• $f:A\times B\to B$ tale che per ogni $(x,y)$ $f(x,y)$ = $y$ si dice proiezione canonica su $B$.
• $f(A)=\{y\in B|\exists x\in A\text{tale che}f(x)=y\}.$ si dice immagine dell’applicazione $f$ e rappresenta tutti i valori che la funzione può assumere

---

• Funzione iniettiva: $f$: $A$ → $B$ se porta punti distinti del dominio su su punti distinti del codominio, di solito viene chiamata funzione “uno a uno”. La cardinalità deve essere così: $|A|\le |B|$
• Funzione surgettiva: $f$: $A$ → $B$ una funzione che associa ad ogni elemento di B (codominio) almeno un’elemento di A(dominio). La cardinalità deve essere così: $|A|\ge |B|$
• Funzione biiettiva:$f$: $A$ → $B$ se una funzione è sia iniettiva che surgettiva

Nota bene

1. Una funzione iniettiva può avere elementi del codominio che non vengono raggiunti.
2. Una funzione suriettiva, invece, raggiunge tutti gli elementi del codominio.
3. La corrispondenza biunivoca è una relazione tra due insiemi che stabilisce un legame univoco tra gli elementi di un insieme e quelli di un altro. In termini formali è una funzione biiettiva.

---

Cardinalità di un insieme: definita come il numero di elementi che appartengono all’insieme

Dimostrazione

Teorema Se $A$ e $B$ sono due insiemi finiti ed esiste una funzione iniettiva $f:A\to B$, allora la cardinalità di $A$ è minore o uguale alla cardinalità di $B$, cioè $|A|\le |B|$ Dimostrazione Si considera l’immagine $f(A)$, cioè l’insieme di elementi di $B$ a cui $A$ viene mappato. Poiché $f$ è iniettiva, ogni elemento di $A$ corrisponde a un elemento unico di $f(A)$, quindi $\mid A\mid =\mid f(A)\mid$. Tuttavia, $f(A)$ è un sottoinsieme di $B$ (cioè tutti gli elementi di $f(A)$ appartengono a $B$), quindi $\mid f(A)\mid \le \mid B\mid$. Da qui segue che $|A|\le |B|$.

---

Proprietà delle relazioni ^e57522 Sia dato un insieme $U$ diremo che una relazione $R(x,y)$ definita in $U\times U$ è:

• Riflessiva: se $\forall x\in U$ risulta vero che $R(x,x)$.
• Simmetrica: se $\forall x,y\in U$ risulta vero che $R(x,y)$ e anche $R(y,x)$
• Transitiva: se $\forall x,y,z\in U$ risulta vero che $R(x,y)$ e $R(y,z)$ allora ci deve essere anche una $R(x,z)$
• Antisimmetrica: $\forall x,\forall y\in U$ risulta vero che $R(x,y)$ e $R(y,x)$ $\to x=y$ Una relazione che è sia riflessiva, simmetrica e transitiva si dice relazione di equivalenza e si indica cosi: $x\approx y$.

---

Classe di equivalenza: Dato un insieme $U$ e una relazione di equivalenza su $U$, la classe di equivalenza di un elemento $x\in U$, indicata con $[x]$, è il sottoinsieme di $U$ formato da tutti gli elementi equivalenti a $x$: $[x]=\{y\in U|y\sim x\}.$

Dimostrazione

Teorema Due classi di equivalenza o sono disgiunte o coincidono. Dimostrazione Siano $[x]$ e $[z]$ due classi di equivalenza e supponiamo che esse abbiano un elemento $w$ in comune: pertanto è $w\approx x$ e $w\approx z$. Allora, per la proprietà transitiva è $x\approx z$. Sia ora $y\in [x]$, cioè $y\approx x$. Per la proprietà transitiva è $y\approx z$, cioè $y\in [z]$. Quindi, $[x]\subseteq [z]$. Analogamente si dimostra che $[z]\subseteq [x]$. Quindi possiamo dire che se due classi di equivalenza non sono disgiunte allora devono necessariamente coincidere.

---

Vari ordinamenti delle relazioni

• Si dice di preordinamento una relazione binaria assegnata in un insieme che goda della proprietà riflessiva e transitiva.
• Si dice ordinata una relazione binaria assegnata in un insieme che goda della proprietà riflessiva, transitiva e antisimmetrica.

---

Massimi e minimi In un insieme, non sempre tutti gli elementi sono confrontabili. Il massimo/minimo è l’elemento più grande/piccolo di tutti, mentre il massimale/minimale è l’elemento più grande/piccolo tra tutti gli elementi confrontabili

---

Problema dell’hitting set Siano $U$ un insieme finito, $H\subseteq U$, e sia $A$ una famiglia di sottoinsiemi di $U$ tutti diversi dall’insieme vuoto. Diciamo che $H$ è un hitting set ($HS$) per $A$ se e solo se per ogni $A\in A$ si ha $A\cap H$ $\ne$ ∅. Hitting set minimo e minimale: Siano $U$ un insieme finito, $H\subseteq U$, e sia $A$ una famiglia di sottoinsiemi di $U$ tutti diversi dall’insieme vuoto. Se $H$ è un hitting set e per ogni $x\in H$ l’insieme $H\backslash \{x\}$ non è un hitting set, diciamo che $H$ è un hitting set minimale. Se $H$ è un hitting set tale che $|H|=min\{|K|:K$ è un hitting set $A\}$ allora $H$ è un hitting set minimo

Parte 2

Numeri Interi

---

L’insieme dei numeri naturali viene definito da:

• Esiste un numero naturale 0
• Ogni numero naturale ha un successore denotato come $S(a)$
• Non esiste numero naturale il cui successore è 0
• Numeri naturali distinti hanno successori distinti

---

Assioma del buon ordinamento: Introducendo la funzione successore $S(a)$ è possibile definire una relazione di buon ordinamento sui numeri naturali, questo viene chiamato assioma del buon ordinamento quindi dato un generico insieme $S$ esiste un elemento minimo $s\in S$

---

Principio di induzione: Sia $P$ una proprietà sui numeri naturali. Il principio di induzione afferma che se $P$ vale per il numero $0$ (caso base) e, inoltre, se la proprietà $P$ vale anche per il successore di ogni numero naturale per cui vale, ossia se $P(n)$ è vera allora è vera anche $P(n+1)$ allora la proprietà $P$ è posseduta da tutti i numeri naturali.

Dimostrazione

Teorema: Sia $P$ una affermazione riguardante i numeri naturali. Se:

1. $P(0)$ è vera ed inoltre
2. per ogni numero naturale $n$ se $P(n)$ è vera allora è vera anche $P(n+1)$

Dimostrazioni: Ragioniamo per assurdo e sopponiamo falsa la tesi, ossia supponiamo che esiste almeno un numero naturale $n$ per cui $P(n)$ è falsa, e costruiamo così il seguente insieme:

$S=\{n:n\in \mathbb{R}$ e $P(n)$ è falsa$\}$

Per la nostra ipotesi $S$ non è vuoto. Per l’assioma del buon ordinamento dentro $S$ abbiamo un elemento minimo $s$. Per definizione di $S$, $P(s)$ è falsa, dal teorema sappiamo che $P(0)$ è vera quindi $s\ne 0$. Poiché $S\subset \mathbb{N}$ deve essere $s>0$, essendo $s$ maggiore di 0 ha un predecessore ovvero $s-1$, dal momento che $s-1<s$ abbiamo che $s-1\notin S$ è vera ($s$ è il più piccolo elemento di $S$). Questo implica che per il caso 2 del teorema che se $P(s-1)$ è vera anche $P(s)$ è vera, siamo arrivati ad una contraddizione

Esempio principio di induzione.pdf

---

Aritmetica modulare: Dati due interi $a,b\in Z$, chiamati rispettivamente dividendo e divisore, esistono unici due interi relativi $q,r$, denominati rispettivamente quoziente e resto.

• $+n\mathrm{mod}+m$: dividi $n$ per $m$ e prendi il resto
• $-n\mathrm{mod}+m$: dividi $-n$ per $m$ prendi il resto, calcoli il resto reale cosi: $r=b-r^{\prime }$
• $+n\mathrm{mod}-m$: dividi $n$ per $m$ e prendi il resto
• $-n\mathrm{mod}-m$: dividi $n$ per $m$, prendi il resto e calcoli il resto reale cosi: $r=-n-r^{\prime }$

---

Definizione di divisibilità: Dati 2 interi relativi $n,m\in Z$ si dice che $m$ è un divisore di $n$ $(m|n)$ se esiste un intero relativo $k\in Z$ tale che $n=k\times m$.

---

Numero dispari: un numero dispari ha questa forma: $n=2k+1$

Dimostrazioni

Teorema: la somma dei primi $n$ numeri dispari è $n^2$ Dimostrazione:

• Caso base: $n=1$ e la somma in questo caso è proprio $1=1^2$
• Caso induttivo: Assumendo che la somma dei primi $n-1$ numeri dispari è uguale a $(n-1{)}^2$ e un generico numero dispari è definito con: $n=2k+1$, quindi se aggiungiamo a $(n-1{)}^2$ il numero dispari successivo quindi $2(n-1)+1$ otteniamo:
• $(n-1{)}^2+2(n-1)+1=n^2-2n+1+2n-2+1=n^2$

---

Dimostrazioni

Somma Teorema: Se $a|b$ e $a|c$ allora $a|(b+c)$ Dimostrazione: Dato che $a|b$ esiste $x$ tale che $b=ax$, e dato che $a|c$ esiste $y$ tale che $c=ay$. Quindi $b+c=ax+ay=a(x+y)$ e ponendo $z=x+y$ abbiamo trovato un intero tale che $b+c=az$ dimostrando che $a|(b+c)$.

---

Prodotto Teorema: Se $a|b$ allora $a|bc$ Dimostrazione: Dato che $a|b$ esiste $x$ tale che $b=ax$, quindi $bc=axc$ il che dimostra che $a|bc$

---

Transitività Teorema: Se $a|b$ e $b|c$ allora $a|c$ Dimostrazione: Dato che $a|b$ esiste $x$ tale che $b=ax$, e dato che $b|c$ esiste $y$ tale che $c=yb$. Quindi $by=axy$ ossia $c=axy$ e ponendo $z=xy$ abbiamo trovato un intero tale che $c=az$ dimostrando che $a|c$

---

Quadrato Teorema: Se $a|b$ allora $a|b^2$ Dimostrazione: Dato che $a|b$ esiste $x$ tale che $b=ax$, quindi $bc=axc$ questi dimostra che $a|b\ast b$

---

Combinazione lineare Teorema: Se $a|b$ e $a|c$ allora $a|(hb+kc)$ per ogni $h,k\in Z$ Dimostrazione: Se $a|b$ allora $a|hb$, se $a|c$ allora $a|kc$ ovviamente valgono per ogni $h,k\in Z$ e quindi è vero che $a|(hb+kc)$

---

Proprietà del numero 0 Teorema: Ogni $a\in Z$ è divisore di $0$ Dimostrazione: $a\in Z$ abbiamo che $a\ast 0=0$ quindi $a|0$

---

Antisimmetrica Teorema: Siano $a,b\in Z$ se $a|b$ e $b|a$ allora $|a|=|b|$ ossia $a=\pm b$ Dimostrazione: Dalle ipotesi abbiamo che $b=ax$ e $a=by$. Quindi $a=axy$, raccogliendo a arriviamo ad $a(xy-1)$ questo implica che $a$ sia $0$ oppure che $xy=1$ da questo capiamo che:

• Se $a=0$ allora anche $b=0$ (perché b = 0x)
• Se $xy=1$ allora $a$ o $b$ sono uguali a $\pm 1$

---

Divisori banali Teorema: Siano a $\in$ Z allora $\pm a|a$ e $\pm 1|a$ Dimostrazione: Avendo che $a=a\cdot 1$ oppure che $a=(-a)\cdot (-1)$ possiamo affermare che $\pm a|a$

• Seguendo la definizione capiamo che $a=b\cdot k$ in questo caso $b=\pm a$ il k che soddisfa le nostre equazioni è k = 1 Avendo che $a=1\ast a$ possiamo dire che 1 è sempre un divisore di $a$

---

• Minimo comune multiplo: Dati $a,b\in Z$ si chiama minimo comune multiplo fra $a$ e $b$ un terzo intero positivo $m$ che è il più piccolo multiplo in comune sia di $a$ che di $b$
• Massimo comune divisore: Dati $a,b\in Z$ si chiama Massimo Comune Divisore un terzo intero $d\in Z$ tale che $d|a$ e $d|b$ cioè $d$ è il più grande divisore comune tra $a$ e $b$.

---

Algoritmo di Euclide: questo è il metodo migliore per il calcolo del MCD e si basa sulla seguente osservazione siano $a,b\in \mathbb{N}$ e sia $b\le a$:

• Caso base: Se $b=0$ allora il $MCD(a,b)=a$. Questo perché qualsiasi numero è divisibile per s
• Passo induttivo: Supponiamo che $a=qb+ra$ , dove $q$ è il quoziente intero della divisione di $a$ per $b$, e $r$ è il resto, con $0\le r<b$ allora $MCD(a,b)$ = $MCD(b,r)$

Dimostrazione

Teorema: $MCD(a,b)=MCD(b,r)$ Dimostrazione:

• Se $d$ è un divisore di $a$ e $b$ allora esistono $h$ e $k$ tali che $a=hd=qkd+r$. Quindi $r=d(h-qk)$ e quindi $d$ è anche un divisore di $r$.
• Viceversa, se $d$ è un divisore di $b$ e di $r$ allora esistono $h$ e $k$ tali che $a=qb+r=qkd+hd$ e quindi $d$ è un divisore di $a$ visto che $a=d(qk+h)$

Esempio

$x_1=330$ e $x_2=156$ $x_3=330\mathrm{mod}156=18$ $x_4=156\mathrm{mod}18=12$ $x_5=18\mathrm{mod}12=6$ $x_6=12\mathrm{mod}6=0$ Quindi $MCD(330,156)=6$. Da questo capiamo che il minimo comune divisore tra 2 numeri può essere calcolato trovando ripetutamente il modulo tra b ed il resto

---

Numero primo: si definisce primo un numero che ha come divisori 1 e se stesso. Numeri coprimi: Due numeri $a,b$ si dicono comprimi se MCD(a,b) = 1 e quindi esistono $h,z$ tali che $(a\cdot h+b\cdot k)=1$

Dimostrazione

Teorema: Due numeri interi consecutivi sono coprimi Dimostrazione: Siano $n$ e $n+1$ due numeri interi consecutivi, allora per $h=1$ e $k=-1$ abbiamo $1=h\times (n+1)+k\times n$

Teorema: Siano $a,b,c\in Z$ tali che $c|a\ast b$ con $c$ ed $a$ coprimi allora $c|b$ Dimostrazione: Siano $a,b,c\in Z$ tali che $c|a\cdot b$ con $c$ e $a$ coprimi. Quindi, esiste $h$ tale che $hc=ab$ ed esistono $k,k\prime$ tali che $1=ka+k\prime c$. Moltiplicando per $b$ ambo i termini dell’ultima uguaglianza otteniamo $b=kab+k\prime cb$ da cui $b=khc+k\prime cb=c(kh+k\prime b)$ e quindi $c|b$

Teorema: Siano $a,b,c\in Z$ tali che $a|c$ e $b|c$, se $a$ e $b$ sono coprimi allora $a\times b|c$ Dimostrazione: Siano $a,b,c\in Z$ tali che $a|c$ e $b|c$, ed $aeb$ coprimi. Allora esistono $h,k,h\prime ,k\prime$ tali che $c=ah$, $c=bk$, e $1=ah\prime +bk\prime$. Moltiplicando per $c$ ambo i termini dell’ultima uguaglianza otteniamo $c=ah\prime c+bk\prime c=ah\prime bk+bk\prime ah=ab(h\prime k+k\prime h)$ e quindi $ab|c$.

---

Fattorizzazione degli interi: ogni intero $n>1$ si può esprimere come prodotto di numeri primi positivi ed in modo unico.

Dimostrazione

Teorema: preso un qualunque numero $n>1$ esiste una fattorizzazione di $n$ Dimostrazione: Se per assurdo esistessero interi > 1 che non sono prodotto di numeri primi positivi potremmo costruire l’insieme

• $S=\{n:n\in N,$ non prodotto di numeri primi $\}$

Per l’assioma del buon ordinamento, dentro questo insieme abbiamo un minimo che chiameremo $s$, $s$ non è primo (perché senno sarebbe un prodotto di numeri primi positivi) quindi vuol dire che ha almeno un divisore non banale positivo chiamato $d$, avendo un divisore vuol dire che esiste un intero positivo $c$ che moltiplicato per $d$ ci da $s$, Poiché, $c$ ed d sono minori di $s$, che ricordiamo è il più piccolo elemento in $S$, allora $c$ e $d$ sono prodotti di primi positivi, e quindi anche $s$ lo è

---

Teorema: la fattorizzazione è unica Dimostrazione: Se $n=p_1\cdot p_2\cdots p_r=q_1\cdot q_2\cdots q_s$ dobbiamo dimostrare che $r=s$ e lo facciamo in questo modo:

• Caso base: $r=1$ Se $n=p_1$ allora $n$ è primo, da $p_1=q_1\cdot q_2\cdots q_s$ otteniamo che $s=1$ e $q_1=p_1$
• Caso induttivo: supponendo che sia vera questa tesi per r, dimostriamola per r+1, quindi: $n=p_1\cdot p_2\cdots p_{r+1}=q_1\cdot q_2\cdots q_s$ , dal caso base sappiamo che $q_1$ è divisore di $p_1$ e che quindi dividendo membro a membro per $p_1$ otteniamo $p_2\cdots p_r\cdot p_{r+1}=q_2\cdots q_s$ da questo capiamo che $r=s-1$ e quindi che $s=r+1$ quindi i fattori coincidono a meno dell’ordine e quindi che sono uguali.

---

Teorema di Euclide: i numeri primi sono infiniti

Dimostrazione

Teorema: i numeri primi sono infiniti Dimostrazione: Supponiamo che ci sia un numero finito di numeri primi. Se così fosse, potremmo elencarli tutti. Chiamiamo questi numeri primi $p_1,p_2,\dots ,p_n$, dove $p_1=2$, $p_2=3$, e così via fino a $p_n$ , che rappresenterebbe l’ultimo numero primo. Ora definiamo $h=p_1\cdot p_2\cdots p_n+1$, per costruzione, $h$ è maggiore di tutti i numeri primi $p_1,p_2,\dots ,p_n$, inoltre sappiamo che non è divisibile da nessuno dei numeri primi. A questo punto, possiamo concludere che $h$ o è primo oppure è divisibile da un numero primo non presente nella lista $p_1,p_2,\dots ,p_n$:

• Se $h$ è primo, allora abbiamo trovato un nuovo numero primo che non era incluso nella lista originale, il che contraddice l’ipotesi che $p_1,p_2,\dots ,p_n$ fossero tutti i numeri primi.
• Se $h$ non è primo, allora deve avere un divisore primo che non è nessuno dei $p_1,p_2,\dots ,p_n$, il che ancora una volta contraddice l’ipotesi che $p_1,p_2,\dots ,p_n$ siano tutti i numeri primi.

---

Crivello di Eratostene: Il crivello di Eratostene è un algoritmo utile per calcolare tutti i numeri primi minori o uguali ad un numero prefissato $n$. L’algoritmo funziona in questo modo. Supponiamo di voler calcolare tutti i numeri primi compresi tra $2$ e $n$. Allora

• Scriviamo in sequenza tutti i numeri naturali compresi tra $2$ e $n$.
• Partiamo dal numero $2$, e cancelliamo dalla sequenza tutti i multipli di $2$.
• Ad ogni passo successivo, prendiamo il primo tra i numeri che seguono e che non è stato cancellato e cancelliamo tutti i suoi multipli.
• Quando abbiamo cancellato tutti i multipli del numero più grande che sia minore o uguale a $\sqrt{(}n)$ ci fermiamo. Tutti i numeri rimasti sono primi compresi tra $2$ e $n$. Esempio

---

Radice numerica: dato un numero $n$ la sua radice numerica di $n$, la denotiamo con $\rho (n)$ ed è la somma delle sue cifre reiterata sono ad ottenere una sola cifra

---

Criteri di divisibilità

Esistono delle regole molto semplici per verificare la divisibilità di un numero $a$ per un numero $b$

• Divisibilità per 2: un numero è divisibile per $2$ se è pari
• Divisibilità per 3: un numero è divisibile per $3$ se la somma delle sue cifre è un numero divisibile per $3$
• Divisibilità per 5: un numero è divisibile per $5$ se l’ultima cifra è $0$ o $5$
• Divisibilità per 7: un numero è divisibile per $7$ se $q-2r$ è divisibile per $7$
• Divisibilità per 11: un numero è divisibile per $11$ se $a-b$ è divisibile per 11
• Divisibilità per 9: un numero $n$ è divisibile per $9$ se la sua radice numerica è divisibile per 9, oppure se $n-\rho (n)$ è divisibile per 9.
• Divisibilità per altri numeri primi:
  • $13$ divide n se $q+4r$ è divisibile per $13$
  • $17$ divide n se $q-5r$ è divisibile per $17$
  • $19$ divide n se $q+2r$ è divisibile per $19$
  • $23$ divide n se $q+7r$ è divisibile per $23$
    • $q=$ quoziente della divisione con $10$
    • $r=$ resto della divisione con $10$

Dimostrazione

Teorema: Sia $n$ un numero naturale e sia $m$ la somma delle sue cifre. Allora $n-m$ è divisibile per 9. **Dimostrazione: **Sia $n$ un numero, rappresentato come: $n={\sum }_{i=0}^k{a}_i\cdot 10^i$ dove $a_0,a_1,\dots ,a_k$ sono le cifre del numero $n$, con $a_0$ che rappresenta le unità, $a_1$ le decine, e così via. Ora consideriamo un altro numero $m$, che ha la forma:- $m={\sum }_{i=0}^k{a}_i$ Questo numero $m$ è la somma delle cifre di $n$. La differenza tra $n$ e $m$ è: $n-m={\sum }_{i=0}^k{a}_i\cdot 10^i-{\sum }_{i=0}^k{a}_i={\sum }_{i=0}^k{a}_i\cdot (10^i-1)={\sum }_{i=0}^k{a}_i\cdot 9\cdot b_i=9\cdot {\sum }_{i=0}^k{a}_i\cdot b_i$

---

Dimostrazione

Teorema: $\sqrt{2}$ non è razionale Dimostrazione: Assumendo che esistano 2 numeri naturali $a$ e $b$ tale che $\sqrt{2}=\frac{a}{b}$, assumendo anche che sia ridotta ai minimi termini almeno uno dei 2 è dispari. Elevando al quadrato otteniamo $a^2=2b^2$ essendo $a^2$ il doppio di un altro numero sarà per forza pari, detto ciò anche $a$ è pari è quindi esiste un numero $k$ tale che $a=2k$ da questo avremo allora:

• $2b^2=a^2=4k^2$ e quindi che anche $b$ è pari visto che $b^2=2k^2$

questa affermazione contraddice la nostra ipotesi inziale

---

Aritmetica modulare

Congruenza modulo $m$ Un intero $a\in Z$ è in relazione con $b\in Z$ se $m|(a-b)$ e quindi che $a-b$ è un multiplo di $m$. In modo equivalente potemmo dire che $a$ è in relazione con $b$ se $a\mathrm{mod}m$ = $b\mathrm{mod}m$. Denotiamo questa relazione così:

• $a\equiv b(\mathrm{mod}m)$ se è vera
• $a\not\equiv b(\mathrm{mod}m)$ se è falsa La relazione di congruenza è una relazione di equivalenza:
• Riflessiva: Per ogni $a\in \mathbb{Z}$, è vero che $a\equiv a(\mathrm{mod}m)$
• Simmetrica: Se $a\equiv b(\mathrm{mod}m)$ allora $b\equiv a(\mathrm{mod}m)$
• Transitiva: Se $a\equiv b(\mathrm{mod}m)$ e b ≡ $c(\mathrm{mod}m)$ allora $a\equiv c(\mathrm{mod}m)$

---

Classi di equivalenza definite dalla congruenza: Le classi di equivalenza definite dalla congruenza modulo mmm raggruppano i numeri interi in base al loro resto quando divisi per mmm. Per $m=0$, ogni numero forma una classe distinta perché è uguale solo a sé stesso. Per $m=1$, tutti i numeri appartengono alla stessa classe, dato che ogni numero è multiplo di 1. Per $m=2$, i numeri si dividono in due classi: una con i numeri pari e una con i dispari. In generale, una classe di equivalenza modulo mmm contiene tutti i numeri che danno lo stesso resto quando divisi per m.

---

Definizioni

Teorema: fissato un intero $m>1$ le sue classi di equivalenza sono: $[0{]}_m,[1{]}_m,[2{]}_m,\dots ,[m-1{]}_m.$ Dimostrazione: Sia $a\in Z$ e sia $r$ il resto della divisione intera di $a$ per $m$, ovvero, applicando l’algoritmo di divisione

• $a=qm+r$ con $0\le r<m$.

Dal momento che $a-r=qm$ abbiamo che $a\equiv r(\mathrm{mod}m)$. Quindi, dal momento che $r$ può assumere solo i valori che vanno da $0$ a $m-1$ le classi di equivalenza sono solo quelle dell’enunciato del teorema.

---

Teorema: Le classi definite dalla congruenza sono distinte Dimostrazione: Ragioniamo per assurdo e supponiamo che esistano $x,y\in Z$, $x\ne y$ e $0\le x$, $y<m-1$ tali che $[x{]}_m$ = $[y{]}_m$ . Senza perdita di generalità supponiamo che $x>y$. Dall’ipotesi possiamo scrivere $x-y=km$ cioè $x-y$ è un multiplo di $m$. Da $0\le x,y<m-1$ e $x>y$ segue che $0<x-y<m-1$, che è una contraddizione visto che non esistono multipli di m in tra $0$ e $m-1$.

---

Invarianza rispetto a somma e prodotto: Dato $m\in N$ e dati $a,b\in Z$ tali che $a\equiv b(\mathrm{mod}m)$ allora prendendo $c,d\in Z$ tali che $c\equiv d(\mathrm{mod}m)$ abbiamo che:

• $a+c\equiv b+d(\mathrm{mod}m)$
• $a\ast c\equiv b\ast d(\mathrm{mod}m)$

Dimostrazione

Teorema: Definizione di invarianza rispetto a somma e prodotto Dimostrazione:

1. $(a+c)-(b+d)=(a-b)+(c-d)=(k_1$ + $k_2$)$m$ (da questo capiamo che qualsiasi sia l’ordine delle lettere avremo sempre dei multipli di $m$)
2. Abbiamo $a=b+k_{1}m$ e $c=d+k_{2}m$ quindi $ac-bd=(b+k_{1}m)(d+k_{2}m)-bd=b{k}_{2}m+d{k}_{1}m+k_1{k}_2{m}^2=(b{k}_2+d{k}_1+k_1{k}_{2}m)m$

---

Dimostrazione

Teorema: Per ogni $m\in N,m>1$ prendendo una qualunque sequenza di m interi questa contiene un intero divisibile per m Dimostrazione: Consideriamo allora $m$ interi consecutivi, dove il più piccolo è $n$, Come abbiamo già dimostrato, le classi di equivalenza della relazione di congruenza modulo $m$ sono $[0{]}_m,[1{]}_m,[2{]}_m,...[m-1{]}_m$ , il nostro numero $n$ si trova in una di queste classi di equivalenza, supponiamo stia nella classe $[i{]}_m$ per $0\le i\le m-1$. Quindi $n\equiv i(\mathrm{mod}m)$ ed allora $n+1\equiv i+1(\mathrm{mod}m)$ ovvero $n+1\in [i+1]m$. Notiamo allora che se $i=0$ ovvero $n\in [0{]}_m$ abbiamo dimostrato il teorema. Se invece $i>0$, visto che $0<i<m$ incrementando $i$ esattamente $m-i$ volte, con $m-i<m$ otteniamo che $n+(m-i)\equiv i+(m-i)(\mathrm{mod}m)$ ossia $n+(m-i)\equiv m(\mathrm{mod}m)\equiv 0(\mathrm{mod}m)$. In conclusione, $n+(m-i)$ è il numero multiplo di $m$ nella sequenza di $m$ numeri consecutivi.

---

Esercizi importanti

---

Inverso modulare: anche nell’aritmetica modulare esiste il concetto di inverso modulare. Siano $a,b\in N$ entrambi maggiori di zero. Allora, esiste un elemento $x\in N$ tale che $a\cdot x\equiv 1(\mathrm{mod}b)$ se e solo se $a$ e $b$ sono coprimi. L’elemento $x$ viene chiamato “inverso di $a$ modulo $b$”

Dimostrazione

Teorema: definizione di inverso modulare Dimostrazione:

Funzione di Eulero

Dato $n$ un intero positivo per definire quanti sono i numeri che precedono $n$ e che sono anche comprimi con $n$ dobbiamo usare la funzione di Eulero definita così:

• $\varphi (n)=|\{x:x\in \mathbb{N},0<x\le n,MCD(n,x)=1\}|$ Calcoliamo questo numero in questo modo:

1. Per n numero primo allora $\phi (n)=n-1$
   • Esempio: $\phi (11)=11-1=10$
2. Con n multiplo di un numero primo φ(n) = $n^{k_1}$ - $n^{k_2-1}$
   • Esempio: φ(16) = $2^4$ - $2^3$
3. Con n prodotto di numeri primi $\phi (n)=\phi (k)\times \phi (q)...$ ($k$ e $q$ sono numeri primi)
   • Esempio: $\phi (10)=\phi (2\times 5)=(2-1)\cdot (5-1)=1\cdot 4=4$

---

Dimostrazione

Teorema: Sia n > 1, consideriamo la sua fattorizzazione $n=p_1^{k_1}\cdot p_2^{k_2}\cdot ...\cdot p_m^{k_m}$ allora $\varphi (n)=(p_1^{k_1}-p_1^{k_1-1})\cdot (p_2^{k_2}-p_2^{k_2-1})\cdot \dots \cdot (p_m^{k_m}-p_m^{k_m-1})$ Dimostrazione:

Caso base: se $m=1$ allora $p_1^{k_1}$ sappiamo che è vera

Passo induttivo: Supponiamo il teorema sia vero per ogni intero $n^{\prime }$ la cui fattorizzazione presenta $m-1$ primi diversi e quindi abbiamo che $n^{\prime }=p_1^{k_1}\cdot p_2^{k_2}\cdot ...\cdot p_{m-1}^{k_{m-1}}$ a questo punto la fattorizzazione per $n$ sarà uguale a:

• $n=n\prime \cdot p_m^{k_m}$

dal ipotesi induttiva abbiamo che: $\varphi (n^{\prime })=(p_1^{k_1}-p_1^{k_1-1})\cdot (p_2^{k_2}-p_2^{k_2-1})\cdot \dots \cdot (p_{m-1}^{k_{m-1}}-p_{m-1}^{k_{m-1}-1})$ e quindi $\varphi (n)=\varphi (n^{\prime })\ast (p_m^{k_m}-p_m^{k_m-1})$. Come possiamo notare il teorema vale sia nel caso base, sia nel passo induttivo e quindi il teorema è dimostrato.

---

Teorema di Eulero applicato alla esponenziazione modulare: Siano $n,m$ > $0$, se $MCD(n,m)=1$ allora $n^{\phi (m)}\equiv 1(\mathrm{mod}m)$

---

Altro teorema di Eulero: Se $MCD(a,n)=1$, allora per ogni $x>0$ vale la seguente cosa: $a^x\equiv a^{x\mathrm{mod}\phi (n)}(\mathrm{mod}n)$

---

Piccolo teorema di Fermat: Se $p$ è primo e $MCD(a,p)=1$, ovvero $a$ non è un multiplo di $p$, allora $a^{p-1}\equiv 1(\mathrm{mod}p)$

---

Calcolo dell’inverso modulare: se n ed m sono comprimi, allora esiste l’inverso di n modulo m ossia esiste k tale che $n\ast k\equiv 1(\mathrm{mod}m)$, per calcolare l’inverso di $n$ modulo $m$ è: $(n\mathrm{mod}m{)}^{\phi (m)-1}\mathrm{mod}m$

---

Teoria dei numeri

Numeri perfetti: Un numero si dice perfetto se è la somma di tutti i suoi divisori propri. Esempi: $6=1+2+3$ o $28=1+2+4+7+14$

---

Congettura di Goldbach: la congettura di goldbach afferma che qualsiasi numero pari può essere scritto come somma di due numeri primi, quindi $2n=P_1+P_2$ da questo deduciamo che qualsiasi numero $n\ge 4$ $n=\frac{P_1+P_2}{2}$ si pensa che questa congettura sia vera per la distribuzione dei numeri primi.

---

Congettura di Collatz: la congettura di collatz anche detta congettura $3x+1$ afferma che eseguendo questo algoritmo:

Algoritmo di Collatz 
Leggi un intero x ≥ 1 
while (x > 1) do 
	if x mod 2 == 0 x = x/2; 
	else x = 3 ∗ x + 1; 
end_while

la congettura afferma che l’algoritmo si ferma sempre qualunque sia $x$, ossia non esiste un intero $x\ge 1$ partendo dal quale non si raggiunge mai il valore $1$, ad esempio partendo da 5 l’algoritmo produce le seguenti cifre: $5-16-8-4-2-1$

---

Numeri primi gemelli: I numeri primi gemelli sono coppie di numeri primi che hanno una differenza di $2$, come $(3,5),(5,7)$, ecc.

---

Parte 3

Calcolo combinatorio

Regola della somma: Questa regola ci dice che se vogliamo contare il numero di elementi dell’unione tra due insiemi ci basta sommare la cardinalità dei due insiemi.

---

Regola del prodotto: Questa regola ci dice che se vogliamo contare quanti sono le possibili coppie di elementi, il primo scelto da $A$ e il secondo da $B$ ci basta fare $|A|\ast |B|$.

---

Disposizioni e combinazioni:

---

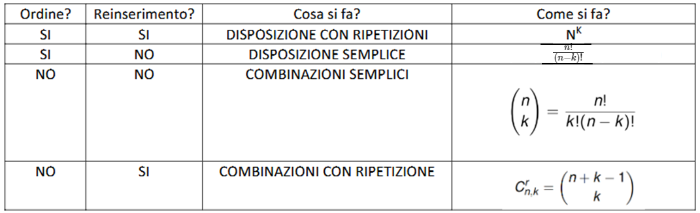
Teorema binomiale: il teorema binomiale è una formula che consente di elevare a qualsiasi numero un binomio così: 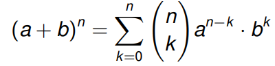Ovvero la sommatoria da $k=0$ fino a $n$ (l’esponente del binomio) della moltiplicazione tra $a^{n-k}\ast b^k$

Dimostrazione

Teorema: definizione teorema binomiale Dimostrazione:

---

Pigeonhole principle: Nella sua forma più semplice, il Principio afferma che se dobbiamo fare entrare $n+1$ piccioni in una piccionaia che contiene $n$ cassette, allora almeno una cassetta dovrà contenere più di un piccione. Più in generale, se abbiamo $n=km+1$ oggetti da sistemare in m contenitori, allora almeno un contenitore dovrà contenere $k+1$ oggetti.

---

Probabilità discrete

Formula generale per la probabilità: $P(A)=\frac{casifavorevoli}{casitotali}$

---

Mutualmente esclusivi: Se due eventi A e B non hanno elementi in comune essi sono detti eventi disgiunti o mutualmente esclusivi perché l’occorrenza dell’uno esclude l’altro.

---

Assiomi della probabilità: Siano $A$ e $B$ due eventi qualsiasi gli assiomi della probabilità sono:

• $0\le P(A)\le 1$
• $P(S)=1$ e $P(\varnothing )=0$
• $P(A\cup B)=P(A)+P(B)-P(A\cap B)$

---

Probabilità condizionata:

• ovvero la probabilità di A, dato B già verificato: $P(A|B)=\frac{P(A\cap B)}{P(B)}$
• probabilità che sia l’evento $A$ che l’evento $B$ accadano: $P(A\wedge B)=P(A)\ast P(B)$

---

Regola di Bayes: se sappiamo che un certo evento E causa certi effetti S, se osserviamo gli effetti S possiamo risalire alla causa $P(B|A)=\frac{P(A|B)\ast P(B)}{P(A)}$

---

Probabilità totale: $P(A)=P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+\cdots +P(A|B_n)P(B_n)={\sum }_{i=1}^{n}P(A|B_i)P(B_i)$ ovvero la sommatoria di tutte le probabilità che A accada se $B_i$ accade

Dimostrazione

Teorema: Definizione di probabilità totale Dimostrazione: Dal momento che gli eventi $B_1,B_2,...,B_n$ sono esaustivi ovvero almeno una di loro si deve verificare. Siccome sono anche mutualmente esclusivi la probabilità che $A$ si verifichi è la somma che sia $A$ che $B_i$ si verifichi ovvero:

• $P(A)=P(A\cap B_1)+\cdots +P(A\cap B_n)$

Dalla definizione di probabilità condizionata sappiamo che per ogni i:

• $P(A\wedge B_i)=P(A|B_i)\cdot P(B_i)$ La formula che usiamo la ricaviamo in questo modo.

A questo punto il teorema è dimostrato

---

Problemi d’urna:

---

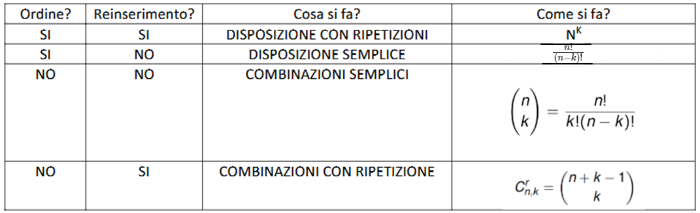
Paradosso del compleanno: Per il Pigeonhole principle potremo dire che in un’aula con 13 persone di sicuro almeno 2 fanno il compleanno lo stesso mese

---

Variabile casuale: Una variabile casuale è una funzione che associa ad ogni risultato possibile di un esperimento casuale un numero reale Valore atteso: Il valore atteso (o media ponderata) di una variabile casuale è il valore medio che ti aspetti di ottenere se ripeti l’esperimento un numero molto grande di volte. 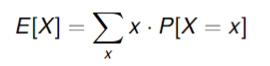Dove:

• $x$ è un possibile valore che la variabile $X$ può assumere
• $P[X=x]$ è la probabilità che $X$ assuma il valore $x$. Una delle proprietà importanti del valore atteso è che è lineare, cioè: $E[X+Y]=E[X]+E[Y]$

Esempio

Domanda: Se lanciamo 2 dadi, qual è il valore atteso del massimo dei 2 valori.

In questo caso abbiamo quindi 36 casi possibili $\{(1,1),(1,2),...,(6,5),(6,6)\}$:

• Di coppie con “6” ne abbiamo 11
• Di coppie con “5” ma senza “6” ne abbiamo 9
• Di coppie con “4” ma senza “5” o “6” be abbiamo 7
• Di coppie con “3” ma senza “4”, “5”, o “6” ne abbiamo 5
• Di coppie con “2” ma senza “3”, “4”, “5” o “6” ne abbiamo 3
• Di coppie con solo “1” ne abbiamo solo 1.

Quindi:

---

Prova di Bernoulli: La prova di Bernoulli è un esperimento probabilistico che ha esattamente due risultati: successo(p) o fallimento(q = 1 - p). Il numero atteso dei numeri di tentativi da fare per ottenere “successo” è dato da 1/p.

---

Paradossi

Paradosso dei Tre Prigionieri: Tre prigionieri (A, B, C) sono condannati a morte, ma uno sarà graziato a caso. Il carceriere sa chi sarà graziato. A chiede al carceriere quale tra B e C sarà giustiziato. Il carceriere risponde “B”. A pensa che la sua probabilità di essere graziato sia passata da 1/3 a 1/2. In realtà, la probabilità che A sia graziato resta 1/3, mentre la probabilità che C sia graziato diventa 2/3.

Parte 4

Teoria dei Grafi

grafo semplice non orientato: denotato con $G=(V,E)$ è formato da:

• un insieme finito di nodi/vertici ($V$)
• un insieme finito di archi ($E$) dove ogni elemento di $E$ è un sottoinsieme di cardinalità 2 di $V$ fatto in questo modo $e_k=\{i,j\}$ con $i,j\in V$

---

grafo semplice orientato: denotato con $G=(V,E)$ consiste:

• un insieme finito di nodi/vertici $(V)$
• un insieme finito di archi $(E)$ in questo caso però gli elementi che appartengono ad $E$ sono delle coppie ordinate, e quindi gli archi hanno un verso.

---

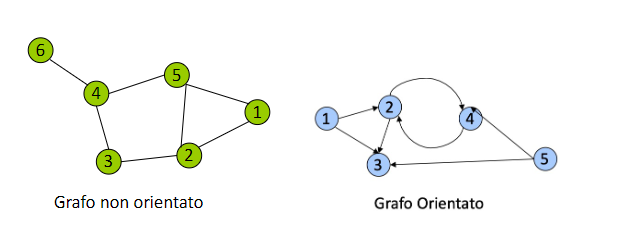
Multigrafo: grafi dove troviamo più di un arco che collega coppie di vertici

---

Grado di un grafo non orientato: Dato un grafo $G=(V,E)$ il grado di un nodo $v$ denotato con $\delta (v)$ è il numero di archi ad esso incidenti, ovvero al numero di archi che lo hanno come uno dei 2 estremi. La somma di tutti i gradi di un grafo è il doppio del numero di archi.

Grado di un grafo orientato: in questo caso abbiamo 2 definizione di grado:

• Grado di ingresso ${\delta }^{-}(v)$: ovvero il numero di archi orientati che “entrano” in $v$
• Grado di uscita ${\delta }^{+}(v)$: ovvero il numeri di archi orientati che “escono” da $v$ La somma di tutti i gradi (ingresso + uscita) di un grafo è il doppio del numero di archi.

---

Grafo regolare: un grafo si dice regolare se tutti i suoi vertici hanno lo stesso grado $r$ da questo possiamo dedurre che: $|V|=\frac{2|E|}{r}$

---

Grafo non orientato completo: diciamo che un grafo è completo se ogni coppia di vertici è connessa da un arco Grafo orientato completo: diciamo che un grafo orientato $G=(V,E)$ è completo se ogni coppia ordinata è connessa da un arco.

---

Torneo: ovvero il grafo orientato ottenuto assegnando uno dei due possibili versi ad ogni arco di $G$, l’arco tra ogni coppia è orientato dal vincitore al perdente.

---

Grafo bipartito: Sia $G=(V,E)$ diciamo che questo arco è bipartito se possiamo partizionare $V$ in 2 insiemi solitamente denotati con $V_1$ e $V_2$ in maniera tale che ogni arco abbia almeno un estremo in entrambi gli insiemi

Grafo bipartito completo: un grafo bipartito si dice completo se definiti $V_1$ e $V_2$ esiste un arco per ogni coppia di vertici, questo tipo di grafo si indica con $K_{n,m}$ dove $n=|V_1|$ e $m=|V_2|$

---

Sottografo: Sia $G=(V,E)$ diciamo che $G^{\prime }=(V^{\prime },E^{\prime })$ è un sottografo di $G$ se:

• $V^{\prime }\subseteq V$
• $E^{\prime }\subseteq E$
• Ogni arco $(u,v)\in E^{\prime }$ ha i suoi estremi entrambi in $V^{\prime }$ Ovviamente un sottografo può essere anche orientato

Sottografo indotto: Sia $G=(V,E)$ e dato $V^{\prime }\subseteq V$, il sottografo che otteniamo se eliminiamo tutti i vertici $\in V^{\prime }$ e tutti gli archi incidenti ad almeno uno dei vertici eliminati viene detto sottografo indotto

---

Grafi isomorfi: Due grafi $G_1=(V_1,E_1)$ e $G_2=(V_2,E_2)$ si dicono isomorfi se esiste una applicazione biunivoca $f$ dall’insieme dei vertici $V_1$ all’insieme dei vertici $V_2$ tale che ($f(u),f(v)$) è un arco di $E_2$ se e solo se $(u,v)$ è un arco di $E_1$. Da questa definizione abbiamo le seguenti conseguenze:

• $|V_1|=|V_2|$ e $|E_1|=|E_2|$
• essendo $f(u)=v$ allora $\delta (u)=\delta (v)$
• essendo $f(u)=v$ allora ${\delta }^{+}(u)={\delta }^{+}(v)$ e ${\delta }^{-}(u)={\delta }^{-}(v)$

---

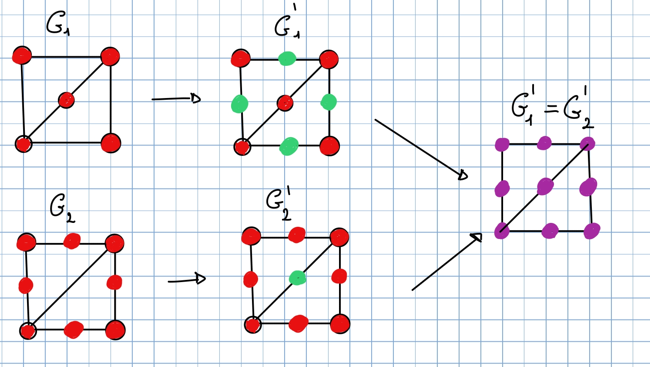
Suddivisone di un arco non orientato: Sia $G=(V,E)$ un grafo non orientato e sia $e=(u,v)$ un arco di G. Una suddivisione dell’arco $e=(u,v)$ è ottenuta introducendo un nuovo vertice w e sostituendo in $G$ l’arco $(u,v)$ con gli archi $e_1=(u,w)$ e $e_2=(w,v)$

Suddivisione di un arco orientato: Sia $G=(V,E)$ un grafo orientato e sia $e=(u,v)$ un arco di G. Una suddivisione dell’arco $e=(u,v)$ è ottenuta introducendo un nuovo vertice w e sostituendo in $G$ l’arco orientato $(u,v)$ con gli archi orientati $e_1=(u,w)$ e $e_2=(w,v)$

---

Omeomorfismo tra grafi: Due grafi orientati $G_1=(V_1,E_1)$ e $G_2=(V_2,E_2)$ si dicono omeomorfi se attraverso una serie di suddivisioni di archi $G_1$ e $G_2$ si possono ottenere due grafi $G_1^{{}^{\prime }}$ e $G_2^{{}^{\prime }}$ che sono isomorfi

---

• Percorso: Un percorso in un grafo $G=(V,E)$ è una sequenza di nodi $v_1,...,v_k$ adiacenti ossia tali che per ogni $1\le i<k$ avrò una coppia $(v_i,v_{i+1})$ che è un arco del grafo. Nel caso di un grafo orientato il percorso deve seguire il verso dell’arco.
• Cammino: Un percorso si dice cammino quando tutti i nodi che attraversa sono differenti.
• Circuito: Un percorso si dice circuito se è del tipo $v_1,...,v_k$ tale che $v_1=v_k$
• Ciclo: Un circuito dove tutti i vertici sono diversi.

---

Grafo aciclico: un grafo si dice aciclico se non possiede cicli

---

Grafo sottostante: ovvero il grafo ottenuto eliminando da un grafo orientato l’orientamento degli archi

---

Vertici connessi: Dato un grafo orientato $G=(V,E)$, diciamo che 2 vertici $u,v$ sono connessi se esiste un cammino a $u$ a $v$

Vertici fortemente connessi: Dato un grafo orientato $G=(V,E)$, diciamo che due vertici $u,v$ sono fortemente connessi se esiste un cammino da $u$ a $v$ e da $v$ ad $u$.

---

Componente connessa: Sia $G=(V,E)$ un grafo. Consideriamo una partizione indotta dalla relazione di connessione tra i vertici $V$ che crea dei sottoinsiemi $V_1,V_2,...,V_k$ dove ciascun $V_i$ rappresenta un insieme di vertici connessi tra loro tramite percorsi all’interno del grafo $G$. Per ogni sottoinsieme $V_i$, definiamo il sottografo $G_i=(V_i,E_i)$, dove $E_i$ è l’insieme degli archi di $E$ che collegano i vertici di $V_i$. Ciascun sottografo $G_i$​ viene detto componente connessa di $G$.

Componente fortemente connessa: Sia $G=(V,E)$ un grafo. Consideriamo una partizione indotta dalla relazione di connessione forte tra i vertici $V$ che crea dei sottoinsiemi $V_1,V_2,...,V_k$ dove ciascun $V_i$ rappresenta un insieme di vertici connessi tra loro tramite percorsi all’interno del grafo $G$. Per ogni sottoinsieme $V_i$, definiamo il sottografo $G_i=(V_i,E_i)$, dove $E_i$ è l’insieme degli archi di $E$ che collegano i vertici di $V_i$. Ciascun sottografo $G_i$​ viene detto componente connessa fortemente connessa di $G$.

---

Grafo connesso: Sia $G=(V,E)$ un grafo non orientato si dice connesso se, per ogni coppia di vertici del grafo, esiste un percorso che li collega. In altre parole, il grafo ha una sola componente connessa, ovvero tutti i vertici appartengono alla stessa componente. Grafo debolmente connesso: Sia $G=(V,E)$ un grafo orientato si dice debolmente connesso se prendendo il suo grafo sottostante quest’ultimo è connesso. Grafo fortemente connesso: Sia $G=(V,E)$ un grafo orientato. $G$ si dice fortemente connesso se ha una sola componente fortemente connessa.

---

Grafo k-connesso: Dato un grafo $G=(V,E)$:

• Il grafo $G$ si dice k-connesso rispetto agli archi se dati comunque due vertici $u,v\in V$ esistono $k$ cammini ad archi disgiunti tra $u,v$.
• Il grafo $G$ si dice k-connesso rispetto ai vertici se dati comunque due vertici $u,v\in V$ esistono k cammini a nodi disgiunti tra $u,v$.

---

Rappresentazione di un grafo non orientato come matrice: Dato un grafo $G=(V,E)$ con $|V|=n$. La matrice di adiacenza del grafo ha dimensione $n\times n$ ed è formata in questo modo:

• $M[i,j]=1$ se i vertici $i$ e $j$ sono connessi da un arco
• $M[i,j]=0$ se i vertici $i$ e $j$ non sono connessi da un arco è importante ricordare che:
• La somma dei valori di ogni riga è il grado del vertice $i$
• Se ci sono degli uno nella diagonale principale vuol dire che nel grafo ci sono dei cappi
• La matrice è simmetrica ovvero per ogni $i$ e $j$: $M[i,j]=M[j,i]$. Rappresentazione di un grafo orientato come matrice: è uguale a quella appena descritta ma dobbiamo fare attenzione al verso delle frecce ed è importante ricordare che:
• La somma degli 1 in ogni riga è il grado in uscita del nodo corrispondente
• La somma degli 1 in ogni colonna indica il grado in entrata del nodo corrispondente
• La matrice non è simmetrica

---

Ciclo in un grafo orientato: Sia $G=(V,E)$ un grafo orientato se per ogni vertice $i\in V$ ${\delta }^{+}(i)>0$ e ${\delta }^{-}(i)>0$ allora il grafo $G$ contiene un ciclo.

Dimostrazione

Teorema: definizione ciclo in un grafo orientato Dimostrazione: Dal momento che ${\delta }^{+}(i)$ > 0 esiste un vertice $i_0$ tale che esiste un arco da $i_0$ a $i_1$, stessa cosa vale per $i_1$ infatti siamo sicuri che esiste un arco da $i_1$ a $i_2$, se iteriamo questo processo sino a quando non abbiamo una sequenza di vertici $i_0,i_1,i_2,...i_n$ tali che ognuno è connesso da un arco al successivo. Se $|V|=n$ per il Pigeonhole Principle almeno 2 di questi n+1 vertici devono coincidere. Questo dimostra il teorema.

---

Algoritmo per trovare un ciclo in un grafo: Sia $M$ la matrice del grafo, ed $M^{\prime }$ la matrice ottenuta da $M$ eliminando la i-esima riga e colonna, sia inoltre $dim(M)$ la dimensione della matrice (il suo numero di righe o colonne)

1. Se controllando la matrice $M$ tutti i vertici del grafo hanno grado in uscita > 0 e grado in entrata > 0 terminiamo e diciamo che il grafo possiede un ciclo
2. Altrimenti, prendiamo un vertice $i$ con grado di uscita/entrata = 0 e lo eliminiamo sia dalla matrice associata al grafo creando la matrice $M^{\prime }$
3. Ripeti passo 2-3
4. Se la $dim(M)$ = 1 ci fermiamo e diciamo che il grafo è aciclico

---

Percorsi tra nodi: La matrice associata $M$ con ogni entrata ci dice se esiste un percorso di lunghezza uno tra due nodi, se voglio trovare i percorsi di lunghezza k basta fare $M^k$ ovvero moltiplicare k-volte per se stessa la matrice $M$. Moltiplicazione tra matrici

---

Rappresentazione di un grafo con le liste di adiacenza: Un grafo può essere rappresentato pure con le liste di adiacenza, ovvero un array i cui elementi sono i nodi e per ogni nodo viene associato un altro array con la lista dei nodi collegati ad esso.

---

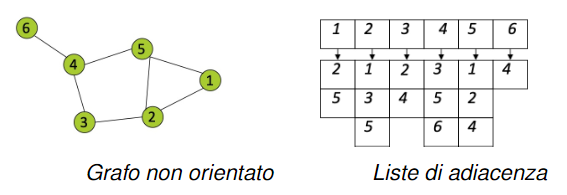
Rappresentazioni standard: Le due rappresentazioni standard per un grafo sono le matrici di adiacenza e le liste di adiacenza. Nel primo caso, si può verificare se due vertici sono connessi da un arco con una sola operazione, ossia controllando che il corrispondente ingresso nella matrice di adiacenza sia uguale ad 1. Nel secondo caso, invece, bisogna scorrere la lista di adiacenza del primo vertice (che può contenere tanti vertici quanti ce ne sono nel grafo) e verificare se il secondo vertice si trova nella lista.

---

Circuito Euleriano: Un circuito euleriano è un circuito chiuso che passa per ogni arco del grafo esattamente una volta Cammino Euleriano: Un grafo possiede un cammino Euleriano se tutti i nodi hanno grado pari tranne 2, che saranno quelli connessi. In questo modo esisterà un cammino che passa per tutti gli archi una sola volta.

---

Cammino Hamiltoniano: Sia $G=(V,E)$ un grafo (digrafo) connesso. Un cammino hamiltoniano di $G$ è un circuito che passa una ed una sola volta per tutti i vertici di $G$. Se il cammino è chiuso, ovvero se è un ciclo, tale ciclo si dice ciclo Hamiltoniano.

---

Grafi pesati: Per poter usare i grafi come strutture dati abbiamo la necessita di associargli un peso, il peso può essere associato agli archi, ai nodi o ad entrambi. Il costo di un cammino quindi può essere dato dalla somma dei costi degli archi, o dalla somma dei costi dei vertici.

---

Rappresentazione dei grafi pesati: i grafi pesati possono essere rappresentati in due modi:

• Peso sugli archi: come quella di un grafo normale, ma al posto di 1 mettiamo il peso dell’arco.
• Peso sui nodi: creiamo una matrice come quella che creeremo per un grafo normale e gli associamo un vettore con i valori dei nodi.

---

Problema del commesso viaggiatore: anche conosciuto come TSP è il problema di trovare un ciclo hamiltoniano che minimizza il costo totale per un grafo pesato 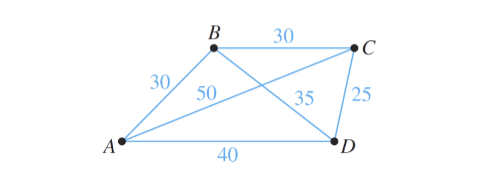Se un commesso viaggiatore deve attraversare tutti e 4 i nodi, partendo da A e tornando ad A, qual è il percorso che minimizza il costo totale, che supponiamo, per esempio, siano distanze in KM? Possiamo risolvere il problema analizzando tutti i cicli hamiltoniani 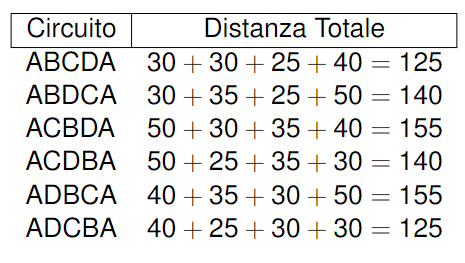Da qui capiamo che ci sono 2 circuiti che il viaggiatore potrebbe usare. All’aumentare dei nodi da attraversare aumenta esponenzialmente il tempo di risoluzione perché si devono banalmente provare più combinazioni. Nessuno ha avuto un idea per risolvere in modo migliore, quindi resta un problema aperto.

---

Grafo planare: Sia $G=(V,E)$ un grafo non orientato diciamo che è planare se può essere raffigurato in modo che non si abbiano archi che si intersecano.

---

Teorema di Kuratowski: Un grafo è planare se non contiene alcun sottografo omeomorfo a $K_5$ o a $K_{3,3}$ Criteri più semplici: Se $G=(V,E)$ è un grafo connesso e planare:

• Se $|V|\ge 3$ allora $|E|\le 3|V|-6$
• Se $|V|\ge 3$ e non ci sono cicli di lunghezza 3 allora $|E|\le 3|V|-4$

---

Facce di un grafo planare: le facce sono il numero di regioni chiuse delimitate da archi. 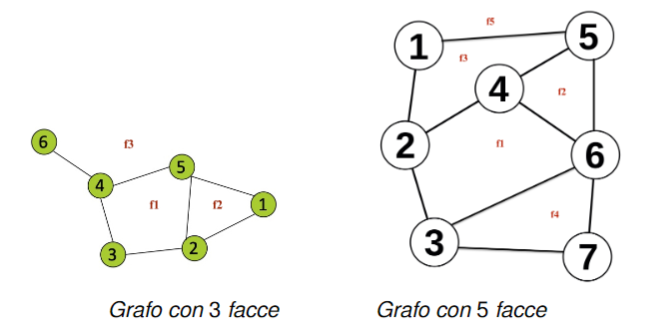Formula di Eulero: se indichiamo con: $v$ il numero di vertici, $e$ il numero di archi e con $f$ il numero di facce allora vale la seguente formula: $v-e+f=2$ dalla quale possiamo ricavare queste formule inverse: $v=e-f+2$ $f=e-v+2$ $e=v+f-2$

---

Dimostrazioni vari teoremi:

Dimostrazione

Teorema Sia $G=(V,E)$ un grafo connesso con $|V|\ge 3$. Supponiamo che $\delta (v)\ge 2$ per ogni $v$. Allora $G$ possiede un ciclo. Dimostrazione Ordiniamo i vertici e chiamiamoli $v_1,v_2,...,v_n$ con $n=|V|\ge 3$. Partiamo da v_1 e costruiamo il cammino più lungo possibile senza ripetizioni di vertici, supponiamo che il cammino più lungo senza ripetizioni sia $v_1,v_2,...,v_k$, dal vertice $v_k$ possiamo ancora raggiungere un altro vertice, dato il grado di almeno 2, dato che ci siamo fermati vuol dire che possiamo raggiungere solo un vertice già visto il che dimostra l’esistenza di un ciclo

Dimostrazione

Teorema Sia $G=(V,E)$ un grafo connesso e aciclico. Allora $|E|=|V|-1$ Dimostrazione Il teorema è banalmente vero se $|V|\le 2$. Supponiamo allora $|V|\ge 3$, essendo il grafo connesso ed aciclico deve esiste un vertice di grado $1$ altrimenti il grafo avrebbe un ciclo, prendiamo questo vertice $v$ e l’arco ad esso incidente il grafo e li rimuoviamo, il grafo indotto $V\backslash \{v\}$ è connesso ed aciclico altrimenti dovremmo avere 2 vertici, $u,w$ che sono connessi solo da un cammino passante per $v$ ma ciò implicherebbe che $v$ ha grado maggiore di $1$ e quindi per induzione ha $|E|=|V|-2$. Aggiungendo $v$ e l’arco ad esso incidente, abbiamo quindi che $|E|=|V|-1$

Dimostrazione

Teorema Sia $G=(V,E)$ un grafo planare connesso, con $v$ vertici, $e$ archi e $f$ facce. Allora $v-e+f=2$ Dimostrazione Se il grafo possiede un ciclo, allora togliamo uno degli archi che completa tale ciclo, il numero di archi e di facce si abbassa allora di una unità e quindi la quantità $v-e+f$ rimane invariata. Ripetiamo tali sottrazioni di archi, sino a quando non eliminiamo tutti i cicli dall’albero, a questo punto avremo un grafo connesso ed aciclico con $e=v-1$ con $f=1$ visto che non ci sono cicli. Quindi $v-e+f=2$

---

Grafo planare massimale: Un grafo planare si dice massimale (o triangolare), se è planare e se aggiungendo un nuovo arco ad una qualunque coppia di vertici il grafo non è più planare. Ogni sua faccia è racchiusa da 3 archi. Dunque un grafo planare massimale ha $3v–6$ archi e $2v–4$ facce.

---

Colorazione di un grafo: Colorare un grafo vuol dire assegnare un colore ad ogni vertice in maniera tale che due vertici collegati da un arco abbiano colori distinti. Il numero cromato del grafo è denotato con $\chi (G)$:

• Grafo completo: in un grafo completo con $n$ vertici $\chi (G)$ = $n$
• Grafo bipartito: 2 colori uno per $V_1$ e uno per $V_2$
• Grafo semplice: con un ciclo che comprende $n$ vertici:
  • n pari: 2 colori diversi
  • n dispari: $2+n\mathrm{mod}2$ colori diversi

---

Teorema di Brooks: Una colorazione ottimale di un grafo $G$ è una colorazione dei vertici di $G$ che usa il numero minimo possibile di colori, ossia $\chi (G)$.

Dimostrazione

Teorema Sia $G=(V,E)$ un grafo connesso con $n$ vertici ${\delta }_1\ge {\delta }_2\ge ...\ge {\delta }_n$ i gradi dei vertici del grafo in ordine crescente. Allora $\chi (G)\le {\delta }_1+1$ Dimostrazione Il Teorema si può facilmente dimostrare per induzione. Se togliamo infatti il vertice di grado maggiore $v_1$, rimaniamo con un grafo con un vertice in meno e colorabile, per ipotesi induttiva, con al più ${\delta }_2+1\le {\delta }_1+1$ colori. Quando aggiungiamo il vertice tolto, il caso peggiore è che i ${\delta }_1$ vertici a lui connessi, siano tutti di colore diverso e quindi gli dobbiamo dare il colore rimasto dei ${\delta }_1+1$.

Teorema di Brooks (versione forte): Sia $G=(V,E)$ un grafo connesso con n vertici, e siano ${\delta }_1\ge {\delta }_2\ge \cdot \cdot \cdot \ge {\delta }_n$ i gradi dei vertici del grafo in ordine decrescente. Se $G$ non è un grafo completo e $G$ non è un ciclo semplice con numero dispari di vertici, allora $\chi (G)\le {\delta }_1$

---

Teorema dei 4 colori: Sia $G=(V,E)$ un grafo planare, allora $\chi (G)\le 4$.

---

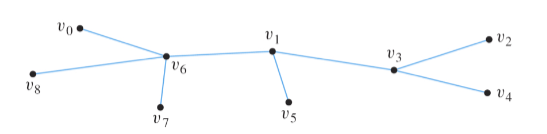
Albero libero: è un grafo connesso e aciclico (denotato di solito con $T$) che ha $|V|-1$ archi, i vertici di grado 1 si chiamano nodi terminali o foglia, mentre i vertici di grafo maggiore di 1 sono detti vertici interni. ((il grafo sotto ha 6 foglie e 3 vertici interni))

---

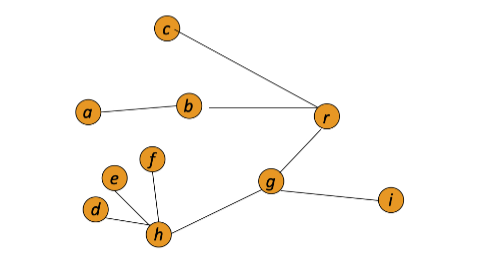
Foresta: è un insieme di uno o più alberi quindi un grafo $G=(V,E)$ aciclico ma non necessariamente connesso. Ogni componente connessa del grafo è un albero della foresta, i vertici di grado 1 sono detti vertici foglia mentre i vertici di grado maggiore sono detti vertici interni. (il grafo sotto ha 6 foglie e 3 vertici interni)

---

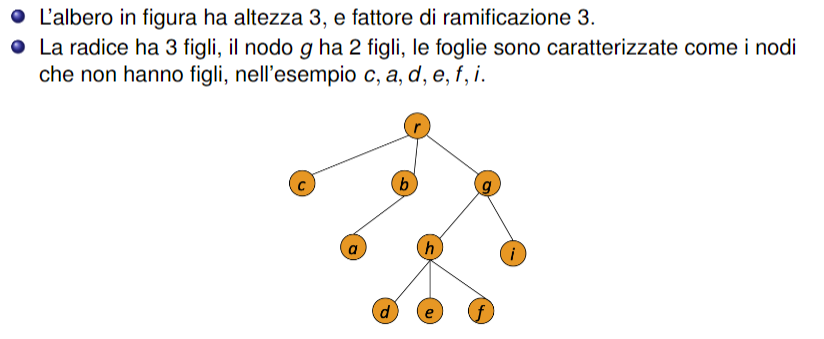
Alberi radicati: Dato un albero $T$ se scegliamo un nodo come radice e immaginiamo di impiantarlo con un chiodo, per gravità tutti gli altri nodi cadranno, così otteniamo un albero radicato:

• Altezza: lunghezza del cammino più lungo dal nodo radice ai nodi foglia
• Fattore di ramificazione: Il fattore di ramificazione di un albero è il numero massimo di figli che un singolo nodo nell’albero può avere.
• i nodi figli di un nodo sono quelli immediatamente sottostanti a esso e direttamente collegati tramite un arco. Il nodo che li collega dall’alto è chiamato nodo padre.

---

Problemi combinatori sui grafi

Due problemi sui grafi che ricadono nella classe N P- hard sono:

1. Il problema della colorazione di un grafo utilizzando il numero minimo di colori;
2. il problema della eliminazione del numero minimo di vertici di un grafo, per renderlo aciclico.